ミラー指数で表された面の図の書き方 ミラー指数が(111)の面 ミラー指数が(121)の面 ミラー指数が(101)の面 ミラー指数で表された面の図の書き方 ミラー指数がの面を図示する場合は、次のとおりである。 まず、結晶中の座標軸を、互いに独立な3つのベクトルで表すと考える。332六方格子のミラー指数 図312六方格子のミラー指数 立方格子との相違→a1,a2,a3,c の4軸を考える点 a1,a2,c 軸をα,β,δで横切る面 a/α :a/β :c/δの最小の整数比h:k:m を求める. 次に最後の指標をl=(hk) のように決める.体心立方格子(BCC) αFe, Mo, W, etc 面心立方格子(FCC) 多結晶体中の結晶粒と方位 集合組織(Texture) 5 ミラー指数 463

第3章 金属の結晶構造
面心立方格子 回折 ミラー指数
面心立方格子 回折 ミラー指数-面心,体 心および六方晶金属の結晶塑性 吉永 日出男* 1緒 言 金属結晶の大部分は面心立方@c),体 心立方(bcc)ま たは稠密六方(hcp)の い・ずれかの結晶構造をもつてい る。化cの中には最も代表的な軽金属であるアルミニウム面心立方格子の特別な場合) のどれになっているかを探す。もちろん、実験値はこの整数値から微妙にずれてい る。これにより、試料の属する格子とMiller指数(整数)の値がわかる。推定され たMiller指数を用いて、格子定数のおおまかな値を求める。


Mukikotaikagaku
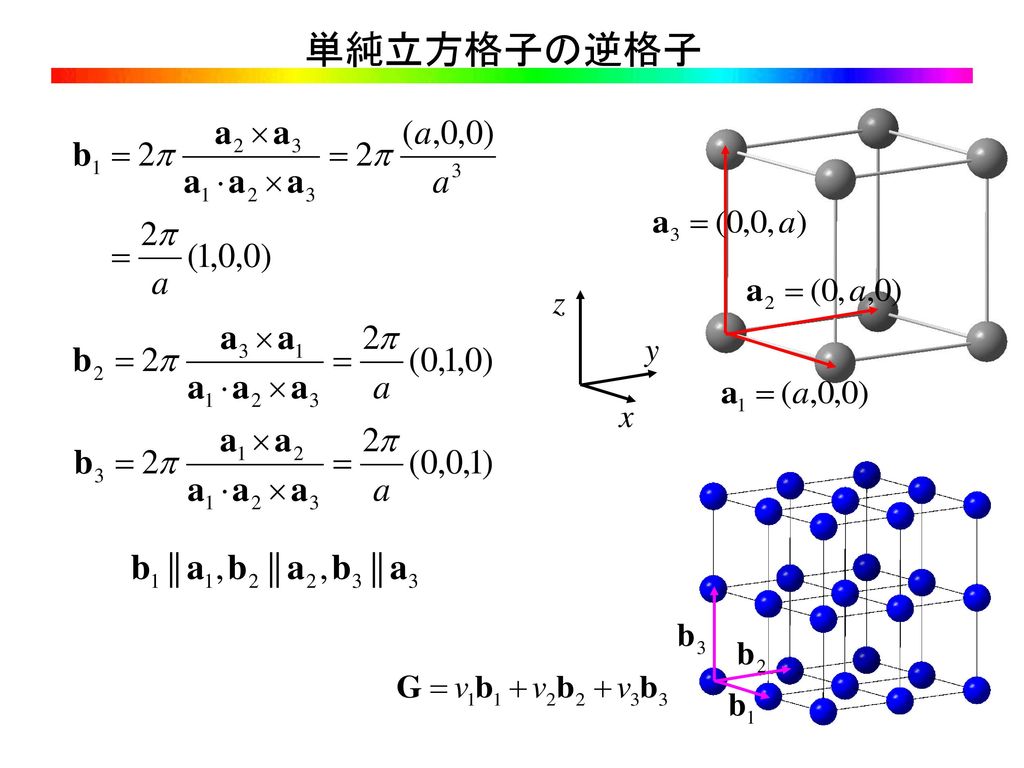
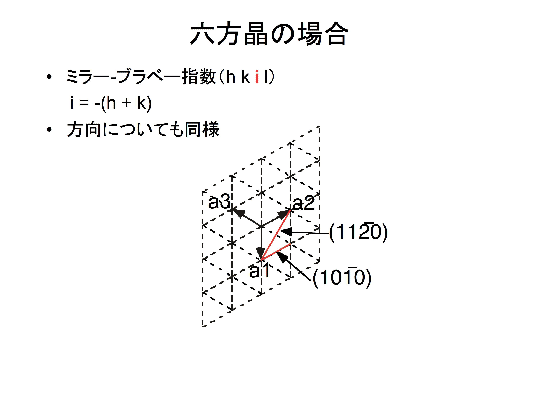
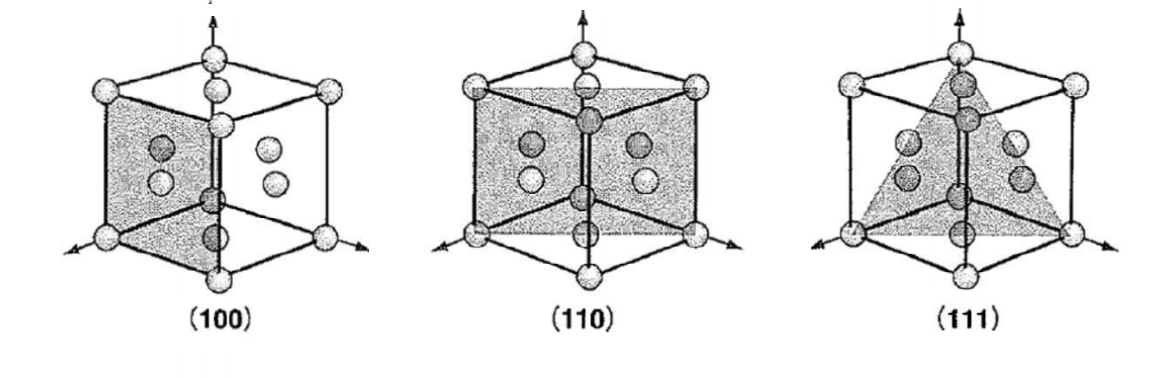
ミラー指数 a c a hcp(0001) hcp(11) どの2次元空間群に属するか? 面心立方格子(最密充填):原子~球(結合の方向性 )17 立方格子と六方格子 立方晶系には単純立方(sc)格子、体心立方(bcc)格子、面心立方(fcc)格子の3種がある。 1) 単純立方格子 単純立方格子は基本単位格子である。直交標系を定義する単位ベクトル x, y, zを用い てa 1 = ax, a 2 = ay, a 3 = az と表す。ミラー指数(面) 5 仮に,上の単位格子が立方晶だとすると(100),(010),(001) は等価な面です.立方体はa,b,c どの軸で も90 度回せばもとにもどりますから,(100) の図をc 軸の回りに90 度回せば(010) の図になります. (010) の図をa 軸の回りに90 度回せば(001) の図になります.図にはありませんが(100) と
面心立方格子(fcc face centered cubic) 六方最密構造(hcp hexagonal closedpacked) 体心立方格子(bcc body centered cubic) ダイヤモンド構造 最密充填構造 配位数=12 最密充填構造 配位数=12 配位数=8 配位数=4 sp3 混成軌道の4ボンドの制約下で最密充填6 ミラー指数その1:結晶における 方向の記述 7 ミラー指数その2:六方晶における ミラー指数 8 面間隔の求め方 9 格子欠陥(原子空孔と転位)・多結晶体 10 x線の発生法・特性x線について 11 ブラッグの条件と面の間隔 12 粉末x線回折による格子定数の求め方隣接する2つの原子面の面間隔dは、ミラー指数hklと格子定数の関数である。立方晶の対称性をもつ結晶では d=a/√(h^2 k^2 l^2) ・・・(1) となる。 質問:「(1)式を証明せよ」と言われたのですが、どうすれば言いかわかりません
面心立方格子と体心立方格子における基本単位格子 面心立方格子 体心立方格子 厳密には,両格子の基本単位格子は,単純三方格子 (菱面体または斜方六面体)になる. 28ミラー指数 (h k j l) をもつ格子面の面間隔を求めよ。 六方晶の格子ベクトルは 逆格子ベクトルは c a x y O A a A ミラー指数 (h k j l) をもつ格子面に対応する逆格子は で 面間隔は 応用波長219ÅのX 線を照射した場合,ミラー指数 (111)の面に対応す る回折角 θ は 5717°であった.この立方晶の格子定数を求めよ.ただし, sin57l7°=084 とす る. (2)面心立方構造および体心立方構造の充填率をそれぞれ


Mukikotaikagaku
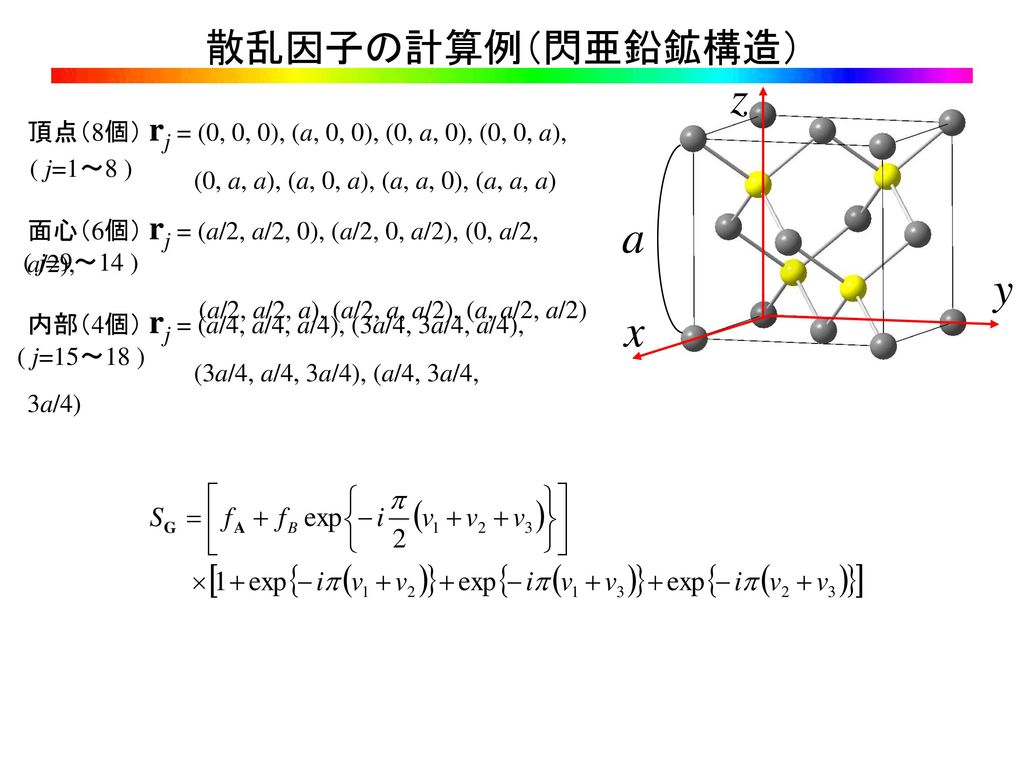


前回の内容 結晶工学特論 第4回目 格子欠陥 ミラー指数 3次元成長 積層欠陥 転位 刃状転位 らせん転位 バーガーズベクトル Ppt Download
To avoid this, cancel and sign in to YouTube on your computer Cancel Confirm 受験生へやる気と効率を上げる問題集の使い方 ( X法) 409 高校化学固体の問題17 面心立方格子は立方晶系にはあるが、正方晶系にはない。その理由について図を用いて説明せよ 答 図4(a) の正方晶系における面心格子を考える。図4(b) のように面心格子の単位胞を2 つ並べると中 に、より小さい単位胞を考えることができる。格子面のミラー指数を求めよ。 図5は面心立方格子を示したもので、原点を O とする。 格子ベクトルは (x, y, z) 座標で である。 (1) 点 A, B, C が乗っている格子面のミラー指数を求めよ。 (2) この格子面の面間隔を求めよ。


ミラー指数 方向 物理のかぎしっぽ


この画像のミラー指数は何かわかりますか またどのように求めたかも教 Yahoo 知恵袋
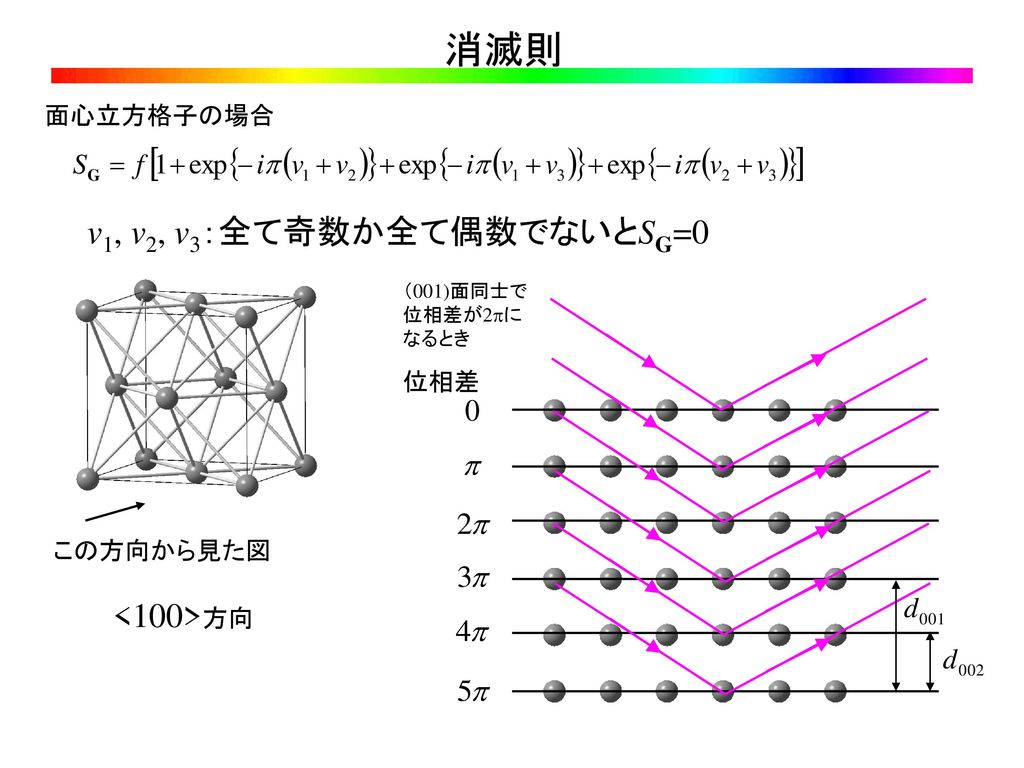
ミラー指数は というふうに,「丸括弧の中の3つの整数」で表示し, それによって任意の格子面を表現することができます. ここでは,任意の格子面をミラー指数で表現する手続きを紹介します.表題の通り,面心立方格子(facecentered cubic lattice)の3Dモデルを作製しました. FCCは高校の化学で習うので,知っている人も多いと思います. ミラー指数などになると高校では習いませんが,材料工学の基礎なので大学の講義で習うことが多いのではないその中でも特に体心立方格子の消滅測 $$ hkl = 2n1 (h,k,lは面指数、nは整数) $$ と面心立方格子の消滅測 $$ hk=2n1 or\\ kl=2n1 or\\ lh=2n1 $$ を解説していきたいと思います。


ミラー指数 面 物理のかぎしっぽ


前回の内容 結晶工学特論 第4回目 格子欠陥 ミラー指数 3次元成長 積層欠陥 転位 刃状転位 らせん転位 バーガーズベクトル Ppt Download
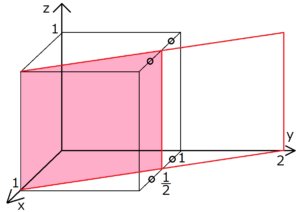
ミラー指数の決め方 とある格子面のミラー指数は、その格子面を無限に延長させたときのx,y,z軸の切片の逆数で表せる。下に具体例を挙げる。 例題 (1,0,0) 上の図の赤く塗られた格子面のミラー指数を考える。 まずx軸の切片は明らかにx=1である。隣接する2つの原子面の面間隔dは、ミラー指数hklと格子定数の関数である。立方晶の対称性をもつ結晶では d=a/√(h^2 k^2 l^2) ・・・(1) となる。 質問:「(1)式を証明せよ」と言われたのですが、どうすれば言いかわかりません6 ミラー指数その1:結晶における 方向の記述 7 ミラー指数その2:六方晶における ミラー指数 8 面間隔の求め方 9 格子欠陥(原子空孔と転位)・多結晶体 10 x線の発生法・特性x線について 11 ブラッグの条件と面の間隔 12 粉末x線回折による格子定数の求め方


ときわ台学 結晶構造 ミラー指数


金属と結晶構造
4 x線回折 1 目的 銅の粉末試料を用いたx 線回折測定を行い、粉末x 線回折の測定方法と測定原理について学ぶ。 また、得られたx 線回折のデータから格子定数の計算や結晶構造の同定を行えるようになる。 あ わせて、結晶を取り扱う上で重要な逆格子やミラー指数の概念についても理解する。面心立方格子と体心立方格子における基本単位格子 面心立方格子 体心立方格子 厳密には,両格子の基本単位格子は,単純三方格子 (菱面体または斜方六面体)になる. 28ミラー指数で表された面の図の書き方 ミラー指数が(111)の面 ミラー指数が(121)の面 ミラー指数が(101)の面 ミラー指数で表された面の図の書き方 ミラー指数がの面を図示する場合は、次のとおりである。 まず、結晶中の座標軸を、互いに独立な3つのベクトルで表すと考える。
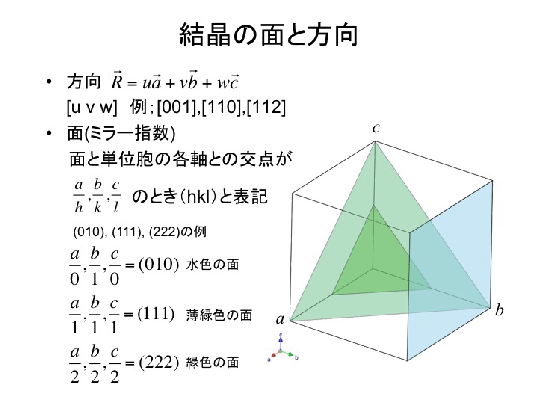


結晶の面と方向の記述方法


放課後化学講義室 X線回折のデータ解析をするプログラム
面心格子h,k,1に 奇数と偶数が混合しているとき 体心格子(hk1)が 奇数のとき このような,消 滅則により現れるはずのない反射を禁制反射と言 います。ニッケル,銅,金 など面心立方晶の場合は,111,0, 2,311,222,400とhk1が すべて奇数か偶数の反射しか現 れません。ダイアモンド格子構造 共有結合性の結晶 シリコン(Si)はダイアモンド格子構造 空間格子は面心立方格子 23 ミラー指数 教科書図1.4 24 ミラー指数練習問題対する面上にも格子点がある(面心単位胞). 単純単位胞(P) 体心単位胞(I) 面心単位胞(F) 8 x y z c a b α β γ a = b = c,α=β=γ=90° ⇨立方晶 a ≠b = c,α=β=γ=90° ⇨正方晶 単位格子:3つの長さ(a, b, c) と3つの角度(α,β,γ)で規定される 原点


x線結晶解析におけるラウエの条件式とブラッグの条件式
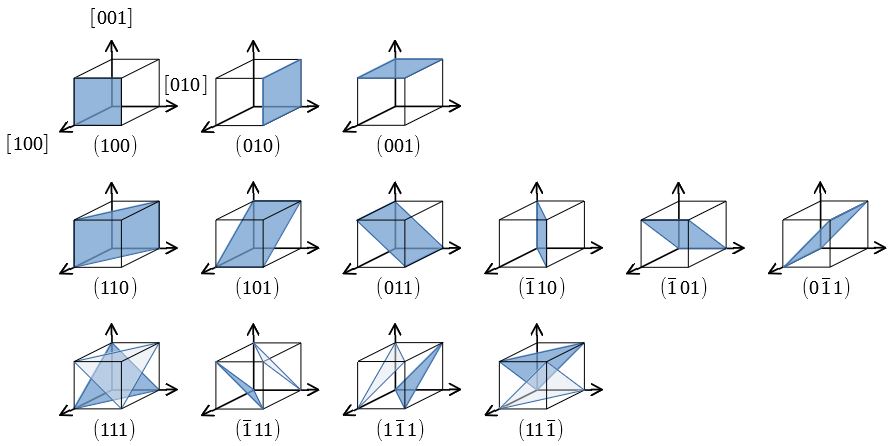


ミラー指数による立方晶 六方晶における面と方向の表し方



面心立方格子 Fcc の逆格子点の導出 化学徒の備忘録


Mukikotaikagaku


ときわ台学 結晶構造 ミラー指数



第3章 金属の結晶構造
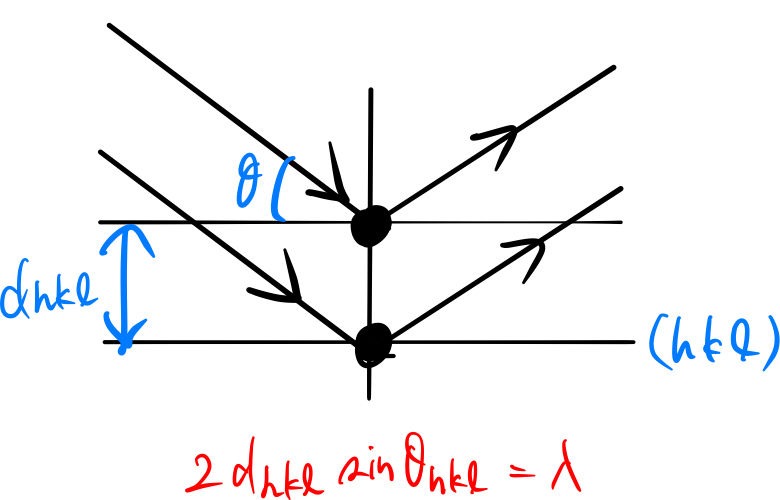


X線回折の解析 計算の基礎 ディフラクトメーター ばたぱら


ときわ台学 結晶構造 ミラー指数
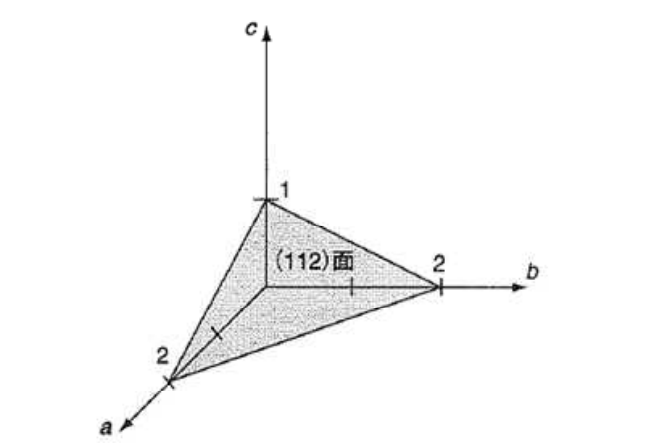


ミラー指数
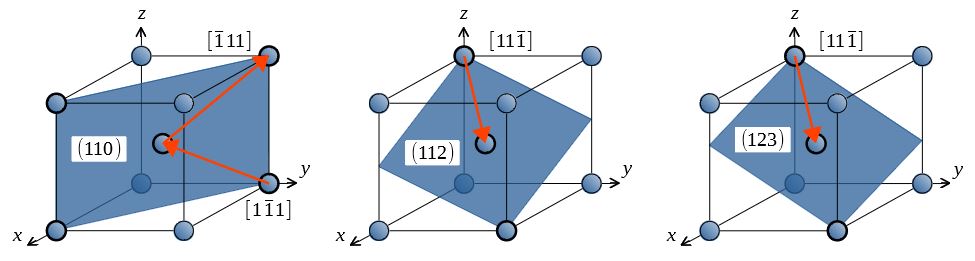


すべり系とシュミットの法則



体心立方格子の 111 面について 体心立方格子の 111 面について質問 化学 教えて Goo


ミラー指数 面 物理のかぎしっぽ



専門 講義 面心立方格子の逆格子とは 大学生 専門学校生 社会人 工学のノート Clear



金属材料の基礎知識 ものづくり まちづくり Btob情報サイト Tech Note



時たま創作ブログ 面心立方 Fcc 格子の結晶面を3dモデルで表示



ミラー指数で表された面の図の書き方 化学徒の備忘録


ミラー指数 方向 物理のかぎしっぽ



立方晶の面指数 ミラー指数 についてです Okwave
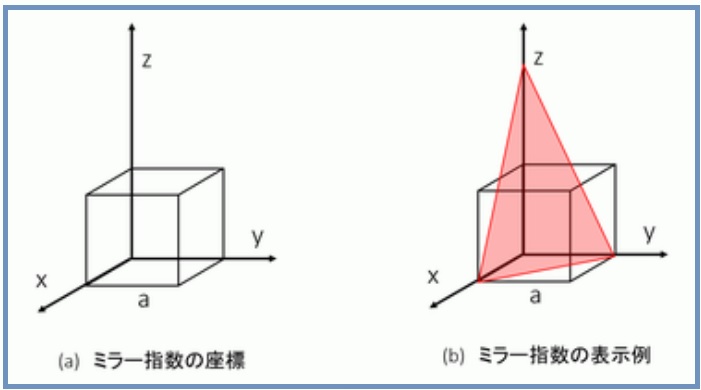


金属 無機材料技術のキーワード解説記事 金属材料基礎講座 その23 ミラー指数 ものづくりドットコム



ミラー指数 Monozukuri Hitozukuri 日本のものづくり


ミラー指数の方向の問題です 何故このようになるのかさっぱりです 解き Yahoo 知恵袋
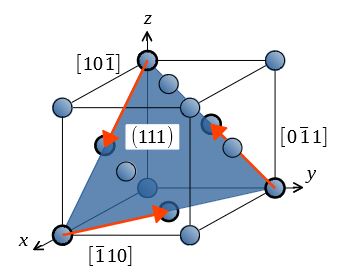


すべり系とシュミットの法則



โน ตของ 専門 講義 結晶構造について ช น Clear
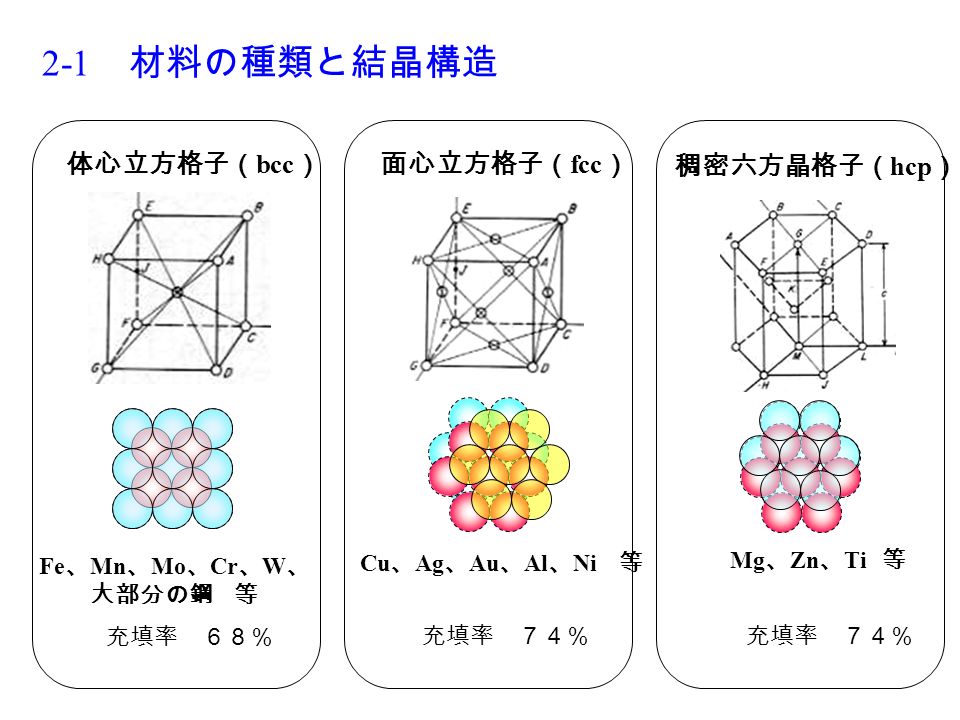


第2章 材料の構造と転位論の基礎 2 1 材料の種類と結晶構造 体心立方格子 c 稠密六方晶格子 Hcp 面心立方格子 Fcc Cu Ag Au Al Ni 等 Mg Zn Ti 等 Fe Mn



ミラー指数 Wikipedia


ミラー指数 面 物理のかぎしっぽ
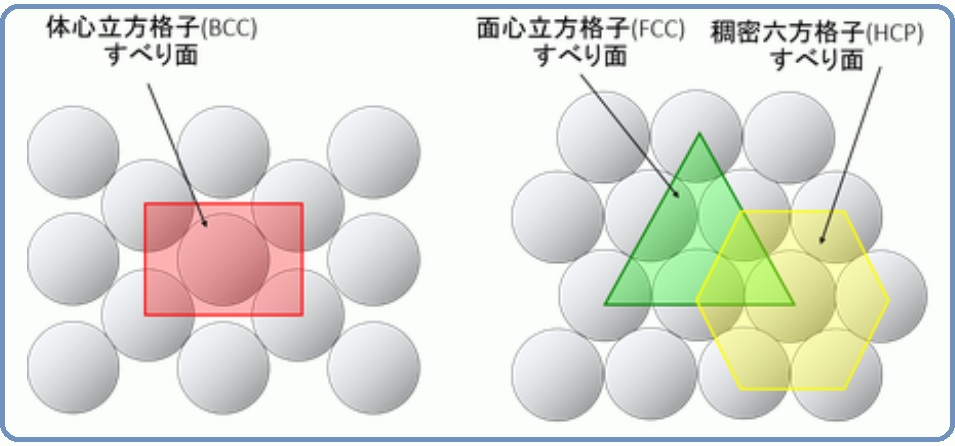


金属 無機材料技術のキーワード解説記事 金属材料基礎講座 その4 すべり系と最密充填構造 ものづくりドットコム


Information



格子についてです 格子についてです Aを通常の格子定数とするとき 物理学 教えて Goo


x線結晶解析におけるラウエの条件式とブラッグの条件式



金属材料の基礎知識 ものづくり まちづくり Btob情報サイト Tech Note


Fundamentals Of Materials Takagi Ikuji



金属材料の基礎知識 ものづくり まちづくり Btob情報サイト Tech Note



金属材料基礎講座 26 福﨑技術士事務所
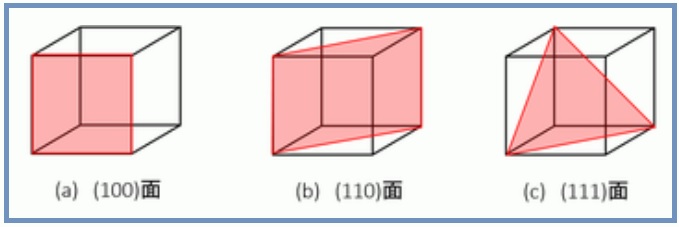


金属 無機材料技術のキーワード解説記事 金属材料基礎講座 その23 ミラー指数 ものづくりドットコム


結晶の面と方向の記述方法



ミラー指数で表された面の図の書き方 化学徒の備忘録


格子面とミラー指数の求め方
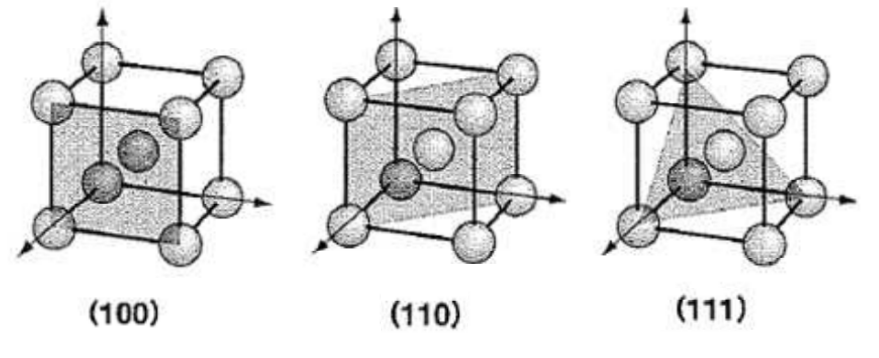


ミラー指数



体心立方格子の基本単位格子 キッテルの固体物理学入門第八版のp 11の 物理学 教えて Goo
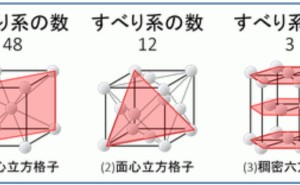


金属 無機材料技術のキーワード解説記事 金属材料基礎講座 その4 すべり系と最密充填構造 ものづくりドットコム


ときわ台学 結晶構造 ミラー指数


前回の内容 結晶工学特論 第4回目 格子欠陥 ミラー指数 3次元成長 積層欠陥 転位 刃状転位 らせん転位 バーガーズベクトル Ppt Download


格子面とミラー指数の求め方


ときわ台学 結晶構造 ミラー指数



金属材料基礎講座 25 福﨑技術士事務所



07 号 金属系膜形成方法及びプログラムを記録した記録媒体 Astamuse
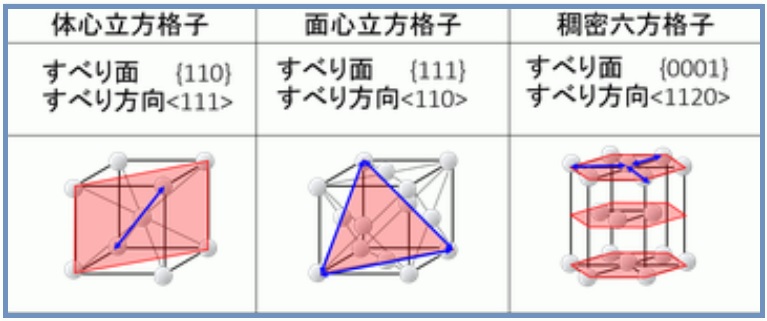


金属 無機材料技術のキーワード解説記事 金属材料基礎講座 その24 ミラー指数の方向 ものづくりドットコム


ミラー指数
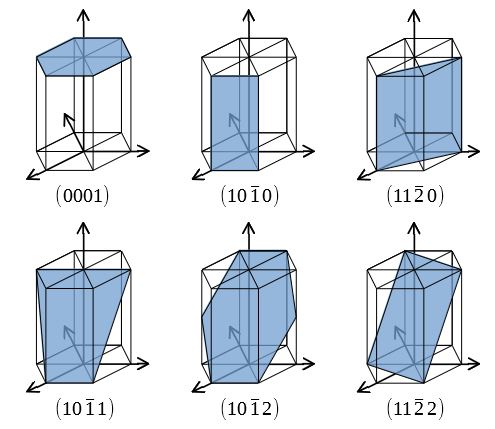


ミラー指数による立方晶 六方晶における面と方向の表し方


Cej Vol 8 No 2 Serial No 15 Reg No 8 10



ミラー指数 Wikipedia
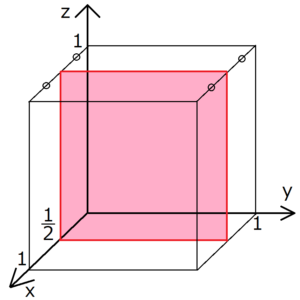


格子面とミラー指数の求め方



ミラー指数 Monozukuri Hitozukuri 日本のものづくり
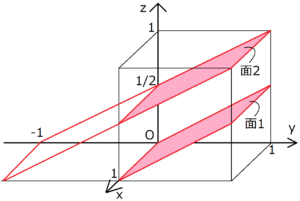


格子面とミラー指数の求め方
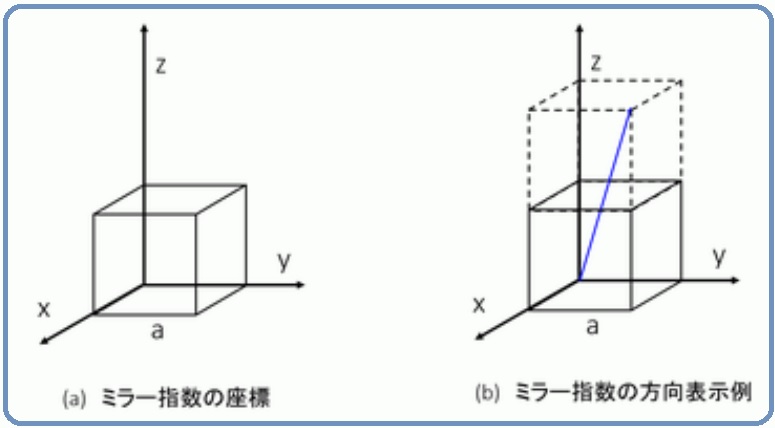


金属 無機材料技術のキーワード解説記事 金属材料基礎講座 その24 ミラー指数の方向 ものづくりドットコム



ミラー指数 Monozukuri Hitozukuri 日本のものづくり
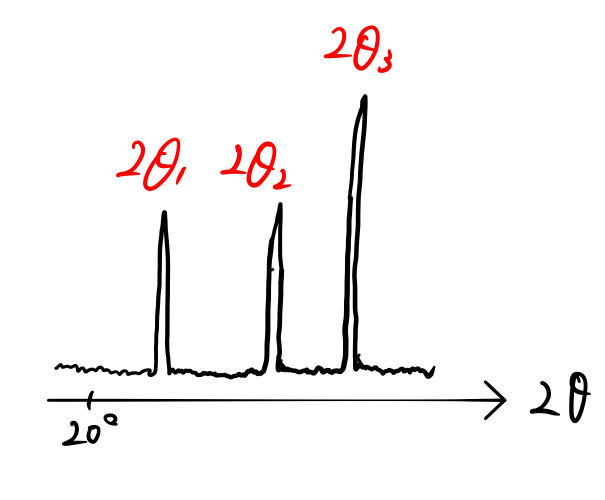


X線回折の解析 計算の基礎 ディフラクトメーター ばたぱら
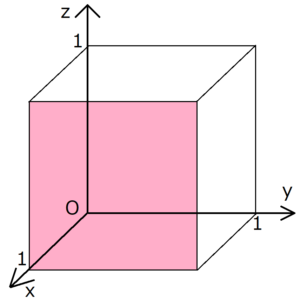


格子面とミラー指数の求め方


ミラー指数 111 と等価なミラー指数って何ですか 1 1 1 Yahoo 知恵袋
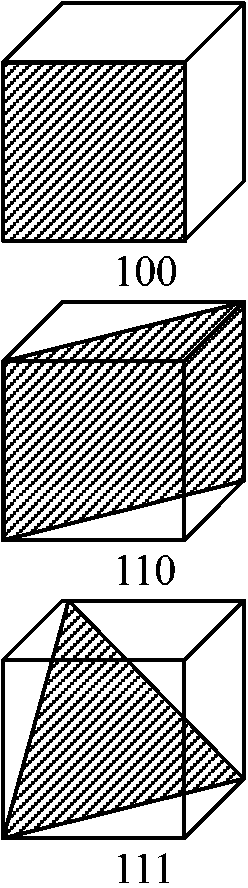


地質学


ときわ台学 結晶構造 ミラー指数



0 件のコメント:
コメントを投稿